
Machine Learning: Algorithmus ist nicht gleich Algorithmus
Im Bereich Machine Learning sind die Anforderungen an Mathematik und Programmierung besonders hoch, da der Zusammenhang von Daten geklärt werde muss.
Algorithmen stehen heute im Zentrum vieler digitaler Produkte und Lösungen – egal ob es sich um autonome Robotersysteme, das Internet der Dinge oder medizinische Diagnosesysteme handelt. Gerade im Bereich Machine Learning sind die Anforderungen an die Mathematik und die Programmierung jedoch besonders hoch. Denn dort ist häufig nicht klar, in welchem Zusammenhang bestimmte Daten zueinanderstehen.
Mit den vorhandenen Daten intelligent auf alle Eingabewerte zu reagieren, ist in diesem Fall nicht nur schwierig, sondern auch zeitaufwendig, vor allem da der Prozess bei jeder Datenänderung wiederholt werden muss. Deshalb empfiehlt sich gerade im Machine Learning der Einsatz von Algorithmen, die je nach Eingabe immer weiter dazulernen und so für die optimale Datenausgabe sorgen.
Gängige Algorithmen – eine Übersicht
Einer der einfachsten Machine-Learning-Algorithmen ist die lineare Regression. Hier wird in einem Datensatz eine Gerade ermittelt, die den geringsten Abstand zwischen den Datenpunkten bildet. Ein Beispiel zeigt Abbildung 2.
Die Polynomanpassung ist eine allgemeinere Variante der linearen Regression und beschreibt die Suche nach einem Polynom eines vordefinierten Grades, das den geringsten Abstand zu allen Datenpunkten hat. Ein Beispiel ist von Grad 0 bis Grad 9 in Abbildung 7 zu sehen. Die lineare Regression ist dabei eine polynomiale Anpassung des Grades 2.
Der Entscheidungsbaum ist ebenfalls weit verbreitet – das Prinzip ist in Abbildung 1 dargestellt: Im Beispielland erwarb die Polizei weiße Autos von einheimischen Produzenten, was dazu führte, dass weiße Autos als Gebrauchtwagen unbeliebt waren. Es könnte sich schließlich um ein gebrauchtes Polizeiauto handeln. Dementsprechend galt es in der Sprache der Informatik einige Fragen zu beantworten, um den erzielbaren Preis zu ermitteln.
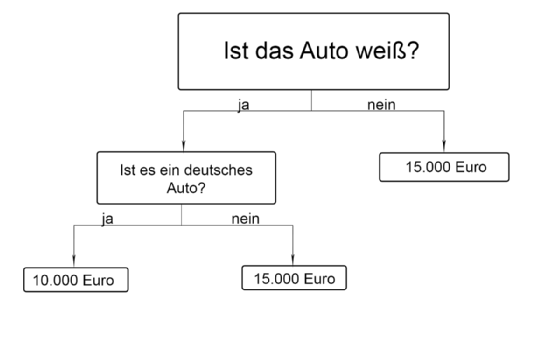
Um zu entscheiden, zu welcher Klasse ein Datenpunkt gehört, braucht es den K-Nearest-Neighbours (KNN)-Algorithmus. Dieser betrachtet die zu K nächsten Nachbarn und prüft, welcher Klasse sie angehören. Der Algorithmus berechnet also in der Lernphase für einen bestimmten Datenpunkt den Abstand zu allen anderen und wählt die K-Datenpunkte aus, die am nächsten liegen. Er zählt im Anschluss, wie viele es von jedem Typ gibt. Die Mehrheit wird als der vorhergesagte Typ gewählt.
Mit Hilfe des K-Means-Algorithmus wird ein geeigneter Mittelpunkt für eine vordefinierte Cluster-Anzahl berechnet und im Anschluss bestimmt, welche Klasse für einen neuen Datenpunkt gewählt wird. Das wird durch die Auswahl des Mittelpunkts, der dem neuen Datenpunkt entspricht, vollzogen.
Bei der Auswahl eines geeigneten Algorithmus sind drei Punkte zu beachten:
1. Nicht jeder Algorithmus ist auf jeden Datensatz anwendbar
Die lineare Regression ist ein gutes Beispiel dafür, dass Machine-Learning-Algorithmen nur in Kombination mit bestimmten Daten brauchbare Resultate liefern. Dieser Algorithmus versucht eine Linie zu finden, die alle Datenpunkte am besten repräsentiert. Deshalb müssen die Eingabewerte rationale Daten sein. Das bedeutet, dass der Abstand zwischen 1 und 2 der gleiche sein muss wie zwischen 4 und 5 sowie 4 der doppelte Abstand von 2.
Ein gutes Beispiel sind hier die Mietkosten im Verhältnis zur Grundfläche der Wohnung (Abbildung 2). Da es sich bei Preis und Größe um Verhältnistypen handelt, funktioniert dieser Vergleich problemlos.
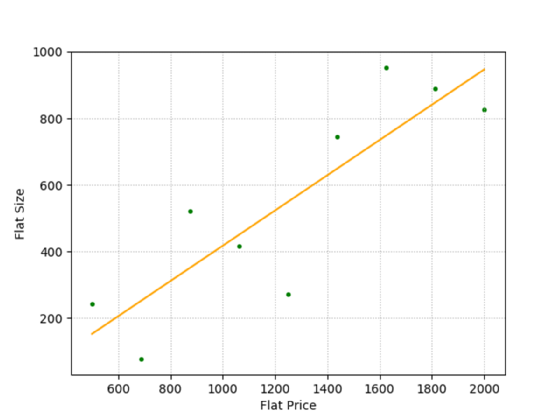
Im Umkehrschluss lässt sich beispielsweise die Farbe des Innenraums nicht mit dem Preis vergleichen, da „Farbe“ keinen rationalen Datentyp beschreibt. Rot ist nicht doppelt so farbig wie grün, genauso wenig wie grün größer ist als rot. Beide Fälle beschreiben keine rationalen Aussagen.
2. Mit der Anzahl der Datenpunkte wächst auch die Laufzeitkomplexität
Nicht jeder Vorhersagealgorithmus hat die gleiche Ausführungszeit. Abhängig von der Anzahl der Datenpunkte, die zum Trainieren benötigt werden, kann sie entsprechend variieren.
Abbildung 3 zeigt beispielsweise Menschen verschiedenen Alters und ihre Entfernung zur nächsten Großstadt. Rot steht dabei für Menschen, die ein Auto besitzen. Grün für Menschen, die keines besitzen.
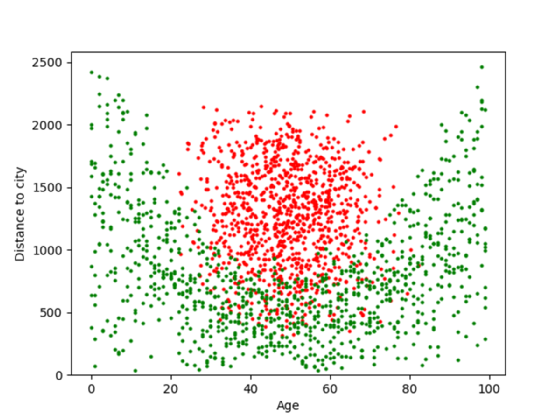
Der KNN-Algorithmus hilft hier vorherzusagen, ob ein bestimmter neuer Datenpunkt ein Auto hat oder nicht. Er platziert den Punkt im Datensatz und sucht nach K Datenpunkten, die dem neuen Datenpunkt am nächsten liegen. Dabei wird der Abstand zwischen diesem Punkt und den Trainingsdatenpunkten berechnet. Die Vorhersagen werden umso genauer, je mehr Trainingsdaten zur Verfügung stehen. Für jeden weiteren Punkt im Trainingssatz dauert die Berechnung des resultierenden Vorhersagealgorithmus jedoch umso länger.
Wenn also eine Vorhersage mit zehn Datenpunkten eine Sekunde dauert, werden für 100 Datenpunkte zehn Sekunden oder länger gebraucht. Ein Algorithmus wie K-Means könnte gerade bei großen Datenmengen zwar zu schnelleren Berechnungen führen, allerdings erfordert dieser kreisförmige Cluster, was in Abbildung 3 nicht der Fall ist.
3. Geringe Datenmengen sorgen für schlechte Ergebnisse
Die Wahl des passenden Algorithmus beeinflusst die Genauigkeit einer Vorhersage stark. Dementsprechend bedeutet es für Machine-Learning-Experten und Data Scientists eine große Herausforderung, aus den vorliegenden Daten die zugrunde liegenden mathematischen Modelle zu entwickeln.
Der Prozess der Modellerstellung lässt sich über den umgekehrten Weg abbilden, indem mit einer einfachen Funktion wie y = -x² + 5x gestartet wird (Abbildung 4).
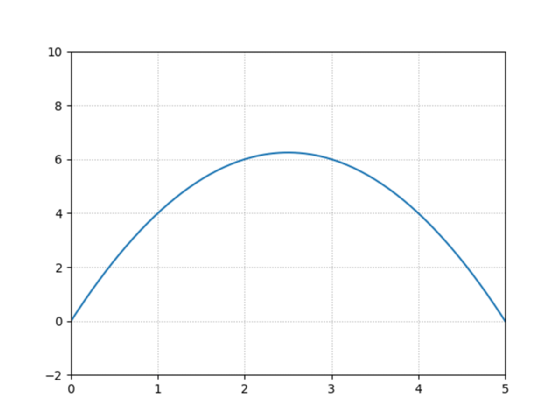
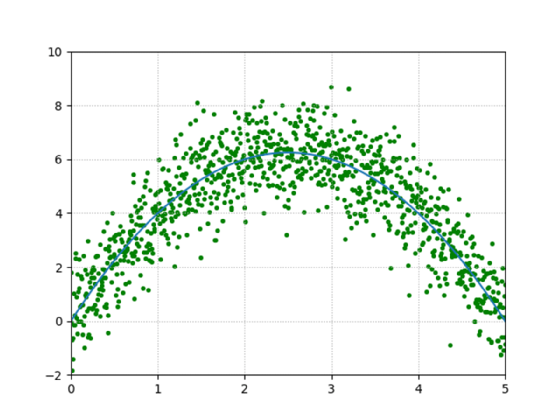
Wenn es um die Messung von Daten aus dem wirklichen Leben geht, ist immer mit Variation oder Datenabweichungen bei den Ergebnissen zu rechnen. Wendet man dieses sogenannte Rauschen auf diese Funktion an, könnten die daraus resultierenden Daten wie in Abbildung 5 aussehen. Die zugrunde liegende Funktion ist jedoch erkennbar.
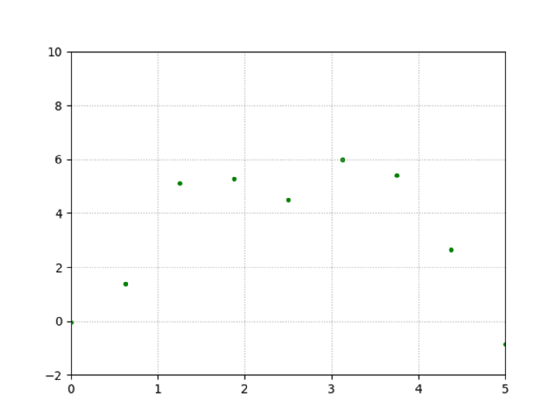
In der Realität steht meist lediglich eine begrenzte Datenmenge bereit, so dass das basierende Modell nicht aufgelöst werden kann. Werden die Datenpunkte auf neun reduziert, ergibt sich folgendes Bild (Abbildung 6):
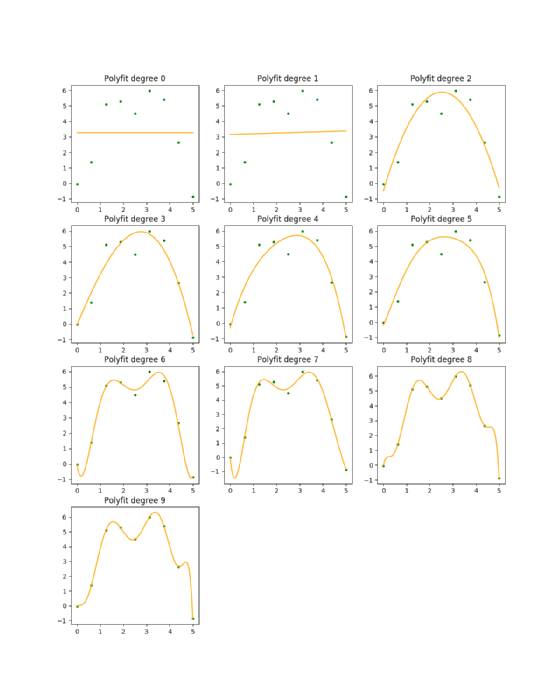
Ein Polynomanpassungsalgorithmus ist der einfachste Weg, die ursprüngliche Funktion herauszufinden. Auf diese Weise lässt sich eine Polynomfunktion einer gewählten Ordnung ermitteln, die den Datenpunkten möglichst nahekommt. Abbildung 7 zeigt zehn Anpassungen für die Ordnungen 0 bis 9:
Hier wird der Vergleich einer Polynomanpassung mit der eigentlichen zugrunde liegenden Funktion dargestellt (Abbildung 8):
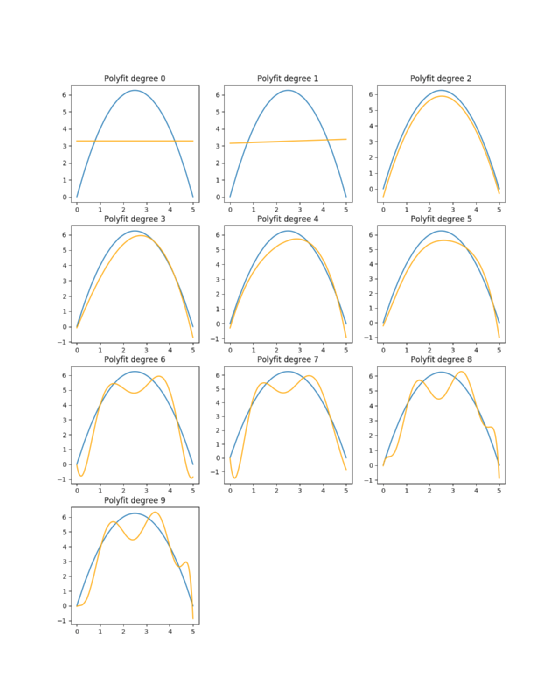
In Abbildung 8 wird deutlich, dass die Grade zwei, drei, vier und fünf Funktionen sind, die dem entsprechen, was die eigentliche zugrunde liegende Funktion ist. Alle anderen Schätzungen sind so weit von der realen Funktion entfernt, dass die Vorhersagen bei der Verwendung dieser Version fehlerhaft wären.

„Im Bereich Machine Learning sind die Anforderungen an die Mathematik und die Programmierung besonders hoch.“
Eugen Klass, OpenText
Problematisch ist hier, dass nicht sicher gesagt werden kann, welche Funktion die Ursprüngliche ist. Bei so wenigen Datenpunkten kann jede Interpretation die Richtige sein.
Vergrößert man die Datenpunktanzahl von zehn auf 1.000, zeichnet sich ein völlig anderes Bild (Abbildung 9).
Hier wurde die Breite der eigentlichen Funktion geändert, um sie von den Polynomanpassungen zu unterscheiden.
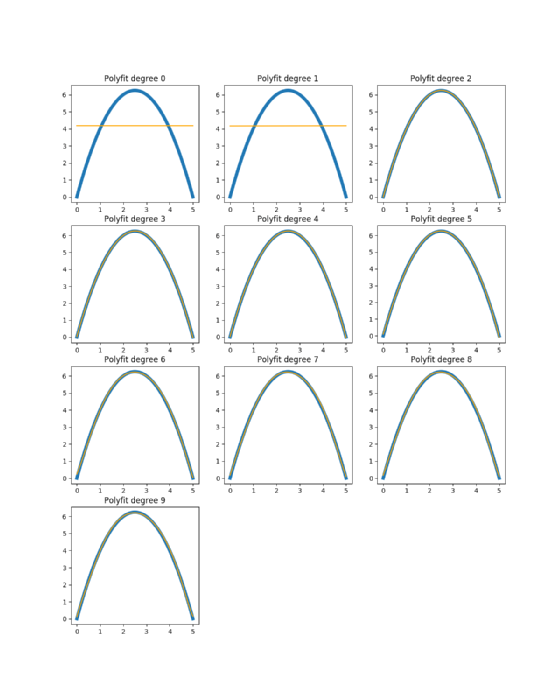
Das zeigt, dass die Wahl des falschen Algorithmus selbst für kleine Mengen an Trainingsdaten die Genauigkeit von Vorhersagen oder Entscheidungen beeinträchtigt.
Daraus lässt sich schließen, dass es keinen universalen Algorithmus gibt, sondern eben verschiedene Ansätze, die mit Trainingsdaten unterschiedlicher Art, Größe und Genauigkeit arbeiten. Die Aufgabe von Datenwissenschaftlern besteht dementsprechend darin, den richtigen Algorithmus zu wählen, der zu den Daten und den entsprechenden Zusammenhängen passt. Das erfordert Erfahrung und Fachwissen.
Über den Autor:
Eugen Klass ist Data Scientist bei OpenText.
Folgen Sie SearchEnterpriseSoftware.de auch auf Twitter, Google+, Xing und Facebook!








