Wie wird Regression beim maschinellen Lernen angewendet?

Was ist Regression beim maschinellen Lernen?

Regression beim maschinellen Lernen ist eine Technik zur Erfassung der Beziehungen zwischen unabhängigen und abhängigen Variablen mit dem Hauptziel, ein Ergebnis vorherzusagen. Dazu wird eine Reihe von Algorithmen trainiert, um Muster zu erkennen, die die Verteilung der einzelnen Datenpunkte charakterisieren. Mit den identifizierten Mustern kann das Modell dann genaue Vorhersagen für neue Datenpunkte oder Eingabewerte machen.

Es gibt verschiedene Arten der Regression. Zwei der gängigsten sind die lineare Regression und die logistische Regression. Bei der linearen Regression besteht das Ziel darin, alle Datenpunkte entlang einer klaren Linie anzupassen. Bei der logistischen Regression geht es darum, zu bestimmen, ob jeder Datenpunkt unterhalb oder oberhalb der Linie liegen sollte. Dies ist nützlich, um Beobachtungen in verschiedene Kategorien wie Betrug/Nicht-Betrug, Spam/Nicht-Spam oder Katze/Nicht-Katze zu sortieren.

„Regression ist ein grundlegendes Konzept in den meisten Statistiken. Maschinelles Lernen ergänzt dies, indem es Algorithmen einsetzt, um diese grundlegenden Beziehungen durch einen automatisierten Prozess zu destillieren“, sagt Harshad Khadilkar, Senior Scientist bei TCS Research und Gastprofessor am IIT Bombay.

„Regression ist das, was Wissenschaftler und Unternehmen bei der Beantwortung quantitativer Fragen verwenden, insbesondere bei Fragen wie zum Beispiel ‚wie viele‘ oder ‚wann‘. Beim maschinellen Lernen wird jede Messung entdeckt, die derzeit nicht in den Daten vorhanden ist“, erklärt er.

Zwei gängige Techniken, die bei der Regression beim maschinellen Lernen verwendet werden, sind die Interpolation und die Extrapolation. Bei der Interpolation besteht das Ziel darin, Werte innerhalb der verfügbaren Datenpunkte zu schätzen. Bei der Extrapolation geht es darum, auf der Grundlage der vorhandenen Regressionsbeziehungen Werte jenseits der Grenzen der vorhandenen Daten vorherzusagen.

Warum ist die Regression beim maschinellen Lernen wichtig?

„Die Regression ist nicht nur für Experten für maschinelles Lernen, sondern auch für alle Führungskräfte in Unternehmen ein wichtiges Konzept, da es sich um eine grundlegende Technik der prädiktiven Analytik handelt“, sagt Nick Kramer, Vice President für angewandte Lösungen beim globalen Beratungsunternehmen SSA & Company. Regression wird häufig für Prognosen verwendet. Indem sie die Art der Beziehung zwischen Variablen aufzeigt, geben Regressionstechniken Unternehmen Einblick in wichtige Themen wie Kundenabwanderung, Preiselastizität und mehr.

David Stewart, Leiter der Abteilung Data Science bei Legal & General, einem globalen Vermögensverwalter, verweist darauf, dass Regressionsmodelle verwendet werden, um Vorhersagen auf der Grundlage von Informationen zu treffen, die uns bereits bekannt sind, was sie für verschiedene Branchen relevant macht. Die lineare Regression, die ein numerisches Ergebnis vorhersagt, kann zum Beispiel dazu verwendet werden, die Körpergröße einer Person auf der Grundlage von Faktoren wie Alter und Geschlecht zu bestimmen. Im Gegensatz dazu kann die logistische Regression die Wahrscheinlichkeit vorhersagen, dass eine Person ein neues Produkt kauft, indem sie ihre früheren Produktkäufe als Indikatoren verwendet.

Wie lineare und logistische Regression funktionieren

Lineare Regression hat eine feste oder konstante Empfindlichkeit gegenüber den Variablen, von denen sie abhängt – sei es bei der Vorhersage von Aktienkursen, dem Wetter von morgen oder der Nachfrage im Einzelhandel. „So führt beispielsweise eine zweifache Änderung einer Variable zu einer bestimmten Abweichung in der Ausgabe“, erläutert Khadilkar. Viele Industriestandard-Algorithmen verwenden eine lineare Regression, wie zum Beispiel die Zeitreihen-Nachfrageprognose.

Die logistische Regression hingegen konzentriert sich auf die Messung der Wahrscheinlichkeit eines Ereignisses auf einer Skala von 0 bis 1 oder 0 Prozent bis 100 Prozent. Der Kerngedanke dieses Ansatzes besteht darin, eine S-förmige Kurve zu erstellen, die die Wahrscheinlichkeit des Eintretens eines Ereignisses anzeigt, wobei das Ereignis – zum Beispiel ein Systemausfall oder eine Sicherheitsverletzung – auf der einen Seite der Kurve sehr unwahrscheinlich und auf der anderen Seite nahezu sicher ist.

Künstliche neuronale Netzwerke in der Regression

„Der Einsatz von künstlichen neuronalen Netzen ist einer der wichtigsten und neuesten Ansätze in der Regression“, sagt Khadilkar. Diese Ansätze nutzen Techniken des Deep Learning, um einige der ausgefeiltesten Regressionsmodelle zu erstellen.

„Sie ermöglichen es uns, Größen mit weitaus komplexeren Zusammenhängen als je zuvor zu anzunähern“, erklärt er. „Heutzutage übernehmen neuronale Netze so ziemlich alle Formen von Regressionsanwendungen.“

Von den oben genannten Ansätzen ist die lineare Regression laut Khadilkar am einfachsten anzuwenden und zu verstehen, aber sie ist nicht immer ein gutes Modell der zugrunde liegenden Realität. Die nichtlineare Regression – zu der auch die logistische Regression und neuronale Netze gehören – bietet mehr Flexibilität bei der Modellierung, aber manchmal um den Preis einer geringeren Erklärbarkeit.

Arten der Regression

Regressionsmodelle liefern zwar eine Antwort, können aber Ungenauigkeiten oder zu starke Vereinfachungen verbergen. Und eine falsche Vorhersage ist oft schlimmer als keine Vorhersage. Es ist wichtig zu verstehen, dass je nach Problem ein Ansatz besser funktioniert als ein anderer.

„Ich verwende häufig die Spitze der Klinge meines Schweizer Taschenmessers, auch wenn der Schraubenzieher effektiver wäre. In ähnlicher Weise sehen wir oft, dass Analysten die Art von Regression anwenden, die sie kennen, auch wenn es nicht die beste Lösung ist“, sagt Kramer.

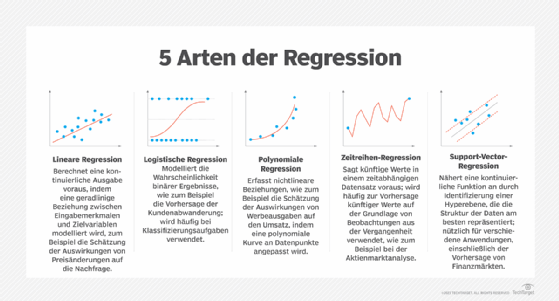
Hier sind fünf Arten der Regression und was sie am besten können:

• Lineare Regressionsmodelle gehen von einer linearen Beziehung zwischen einer Ziel- und einer Vorhersagevariablen aus. Das Modell zielt darauf ab, eine gerade Linie zu bilden, die die Datenpunkte darstellt. Die lineare Regression ist nützlich, wenn eine lineare Beziehung zwischen den Variablen besteht, zum Beispiel bei der Vorhersage von Umsätzen auf der Grundlage von Werbeausgaben oder bei der Schätzung der Auswirkungen von Preisänderungen auf die Nachfrage.
• Logistische Regression wird verwendet, wenn die Zielvariable binär ist oder zwei Klassen hat. Sie modelliert die Wahrscheinlichkeit des Eintretens eines Ereignisses, zum Beispiel ja/nein oder Erfolg/Misserfolg, auf der Grundlage von Vorhersagevariablen. Die logistische Regression wird im geschäftlichen Kontext häufig für binäre Klassifizierungsaufgaben wie die Vorhersage der Kundenabwanderung oder die Erkennung von Transaktionsbetrug verwendet.
• Polynomiale Regression erweitert die lineare Regression, indem sie polynomiale Konzepte wie quadratische und kubische Gleichungen einbezieht, um die Prädiktorvariablen zu formatieren und Fälle zu erfassen, in denen keine direkte lineare Beziehung besteht, wie zum Beispiel die Schätzung der Auswirkungen von Werbeausgaben auf den Umsatz.
• Zeitreihenregression, wie zum Beispiel autoregressive integrierte gleitende Durchschnittsmodelle (Auto-Regressive Integrated Moving Average, ARIMA), berücksichtigen zeitliche Abhängigkeiten und Trends, um zukünftige Werte auf der Grundlage vergangener Beobachtungen vorherzusagen. Diese Modelle sind nützlich für Geschäftsanwendungen wie Absatzprognosen, Nachfragevorhersagen und Börsenanalysen.
• Support Vector Regression (SVR) ist eine Regressionsversion der Support Vector Machines und eignet sich besonders für die Verarbeitung nichtlinearer Beziehungen in hochdimensionalen Räumen. SVR kann für Aufgaben wie die Vorhersage von Finanzmärkten, die Prognose der Kundenabwanderung oder die Vorhersage des Customer Lifetime Value eingesetzt werden.

Anwendungen der Regression

Kramer nennt folgende spezifische Anwendungen der Regression, die häufig in der Wirtschaft eingesetzt werden:

• Absatzprognosen. Vorhersage zukünftiger Verkäufe auf der Grundlage von historischen Verkaufsdaten, Marketingausgaben, Saisonalität, wirtschaftlichen Faktoren und anderen relevanten Variablen.
• Vorhersage des Werts des Kundenlebenszyklus. Schätzung des potenziellen Werts eines Kunden während seiner gesamten Geschäftsbeziehung mit dem Unternehmen auf der Grundlage der bisherigen Kaufhistorie, der demografischen Daten und des Verhaltens.
• Vorhersage der Abwanderung. Vorhersage der Wahrscheinlichkeit, dass Kunden die Dienste des Unternehmens verlassen, auf der Grundlage ihres Nutzungsverhaltens, ihrer Kundeninteraktionen und anderer damit verbundener Merkmale.
• Vorhersage der Mitarbeiterleistung. Vorhersage der Leistung von Mitarbeitern auf der Grundlage verschiedener Faktoren wie Ausbildung, Erfahrung und demografische Daten.
• Analyse der finanziellen Leistung. Verstehen der Beziehung zwischen Finanzkennzahlen (zum Beispiel Umsatz, Gewinn) und wichtigen Einflussfaktoren (zum Beispiel Marketingausgaben, Betriebskosten).
• Risikoanalyse und Betrugserkennung. Vorhersage der Wahrscheinlichkeit von Ereignissen wie Kreditausfällen, Versicherungsansprüchen oder Betrug auf der Grundlage von historischen Daten und Risikoindikatoren.
• Vorhersage von Wartungsarbeiten. Vorhersage der Zeit bis zum Ausfall von kritischen Teilen und Maschinen.

Vor- und Nachteile der Regression

Laut Stewart ist einer der Hauptvorteile von Regressionsmodellen, dass sie einfach und leicht zu verstehen sind. Es handelt sich um transparente Modelle, und es lässt sich leicht erklären, wie das Modell eine Vorhersage trifft.

Ein weiterer Vorteil ist, dass Regressionsmodelle in der Industrie schon seit langem verwendet werden und bekannt sind. So werden beispielsweise verallgemeinerte lineare Modelle in der Versicherungsmathematik häufig verwendet, und ihre Anwendung ist etabliert. „Die Modelle werden von den Aufsichtsbehörden gut verstanden, so dass es einfach ist, fundierte Diskussionen über die Modellimplementierung und die damit verbundenen Risiken, die Unternehmensführung und die Aufsicht zu führen“, erklärt Stewart.

Ihre Einfachheit ist jedoch auch ihre Einschränkung. Regressionsmodelle beruhen auf mehreren Annahmen, die in realen Szenarien selten zutreffen, und sie können nur einfache Beziehungen zwischen Prädiktoren und dem vorhergesagten Wert verarbeiten. Daher sind andere Modelle des maschinellen Lernens den Regressionsmodellen in der Regel überlegen.

Khadilkar ist der Ansicht, dass die Regression den größten Wert als quantitatives Mess-, Interpolations- und Vorhersageinstrument hat – und darin ist sie unglaublich gut. „Ihre Eigenschaften sind bekannt, und wir haben gute Möglichkeiten, unser Vertrauen in unsere Vorhersagen zu quantifizieren“, sagt er. Man kann zum Beispiel Börsenkurse mit einer bestimmten Bandbreite möglicher Schwankungen um die vorhergesagte Menge vorhersagen.

Es gibt jedoch viele Anwendungen, für die die Regression nicht gut geeignet ist. „Zum Beispiel ist sie weniger nützlich, um Gesichter auf Bildern zu erkennen. Sie ist auch nicht geeignet, wenn man versucht, Daten für die Mustererkennung oder die Automatisierung von Entscheidungen zu nutzen“, erläutert Khadilkar. „Der größte Nachteil der Regression ist möglicherweise die Tatsache, dass sie uns nur eine Vorhersage der interessierenden Größe liefert, ohne uns vorzuschlagen, was wir mit den Informationen tun sollen. Das muss der Mensch selbst entscheiden.“