RSA-Algorithmus (Rivest-Shamir-Adleman)
Was ist der RSA-Algorithmus (Rivest-Shamir-Adleman)?
Der RSA-Algorithmus (Rivest-Shamir-Adleman) ist die Grundlage eines Kryptosystems - einer Reihe von kryptografischen Algorithmen, die für bestimmte Sicherheitsdienste oder -zwecke verwendet werden. Dies erlaubt die Verschlüsselung mit öffentlichen Schlüsseln um sensible Daten zu schützen, insbesondere wenn diese über ein unsicheres Netz wie das Internet übertragen werden.
RSA wurde erstmals 1977 von Ron Rivest, Adi Shamir und Leonard Adleman vom Massachusetts Institute of Technology (MIT) öffentlich beschrieben, wenngleich die Entwicklung eines öffentlichen Schlüsselalgorithmus durch den britischen Mathematiker Clifford Cocks im Jahr 1973 vom britischen GCHQ bis 1997 geheim gehalten wurde.
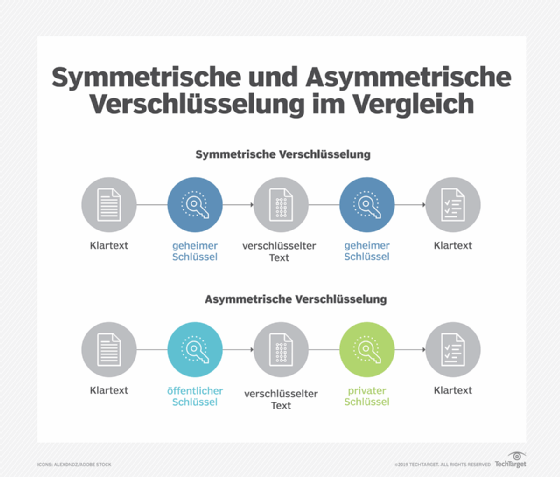
Bei der Public-Key-Kryptografie, auch asymmetrische Kryptografie genannt, werden zwei unterschiedliche, aber mathematisch miteinander verbundene Schlüssel verwendet - ein öffentlicher und ein privater. Der öffentliche Schlüssel kann mit jedem geteilt werden, während der private Schlüssel geheim gehalten werden muss.
Bei der RSA-Kryptografie können sowohl der öffentliche als auch der private Schlüssel eine Nachricht verschlüsseln. Zum Entschlüsseln einer Nachricht wird der entgegengesetzte Schlüssel als der zur Verschlüsselung genutzte verwendet. Diese Eigenschaft ist einer der Gründe, warum RSA der am häufigsten verwendete asymmetrische Algorithmus geworden ist: Er bietet eine Methode zur Gewährleistung der Vertraulichkeit, Integrität, Authentizität und Nichtabstreitbarkeit der elektronischen Kommunikation und Datenspeicherung.
Viele Protokolle, darunter Secure Shell (SSH), OpenPGP, S/MIME und SSL/TLS, nutzen RSA für Verschlüsselungs- und digitale Signaturfunktionen. Es wird auch in Softwareprogrammen verwendet - Browser sind ein typisches Beispiel, da sie eine sichere Verbindung über ein unsicheres Netzwerk, wie das Internet, herstellen oder eine digitale Signatur validieren müssen. Die RSA-Signaturprüfung ist eine der am häufigsten durchgeführten Operationen in vernetzten Systemen.
Warum wird der RSA-Algorithmus verwendet?
Die Sicherheit von RSA beruht auf der Schwierigkeit, große ganze Zahlen zu faktorisieren, die das Produkt aus zwei großen Primzahlen sind. Die Multiplikation dieser beiden Zahlen ist einfach, aber die Bestimmung der ursprünglichen Primzahlen aus der Gesamtsumme - oder das Faktorisieren - wird aufgrund des Zeitaufwands, der selbst mit Supercomputern erforderlich wäre, als undurchführbar angesehen.
Der Algorithmus zur Erzeugung des öffentlichen und privaten Schlüssels ist der komplexeste Teil der RSA-Kryptografie. Zwei große Primzahlen, p und q, werden mit Hilfe des Rabin-Miller-Primzahltest erzeugt. Durch Multiplikation von p und q wird ein Modulus, n, berechnet. Diese Zahl wird sowohl vom öffentlichen als auch vom privaten Schlüssel verwendet und stellt die Verbindung zwischen ihnen her. Ihre Länge, in der Regel in Bits ausgedrückt, wird als Schlüssellänge bezeichnet.
Der öffentliche Schlüssel besteht aus dem Modulus n und einem öffentlichen Exponenten e, der normalerweise auf 65537 gesetzt wird, da dies eine nicht zu große Primzahl ist. Die Zahl e muss keine heimlich gewählte Primzahl sein, da der öffentliche Schlüssel mit allen geteilt wird.
Der private Schlüssel besteht aus dem Modulus n und dem privaten Exponenten d, der mit Hilfe des erweiterten euklidischen Algorithmus berechnet wird, um die multiplikative Umkehrung in Bezug auf den Totalwert von n zu finden.
Wie arbeitet der RSA-Algorithmus?
Alice erzeugt ihre RSA-Schlüssel, indem sie zwei Primzahlen wählt: p=11 und q=13. Der Modulus ist n=p×q=143. Der Totalwert ist n ϕ(n)=(p-1)x(q-1)=120. Sie wählt 7 für ihren öffentlichen RSA-Schlüssel e und berechnet ihren privaten RSA-Schlüssel mit dem erweiterten euklidischen Algorithmus, der ihr 103 liefert.
Bob möchte Alice eine verschlüsselte Nachricht, M, schicken, also erhält er ihren öffentlichen RSA-Schlüssel (n, e), der in diesem Beispiel (143, 7) ist. Seine Klartextnachricht besteht nur aus der Zahl 9 und wird wie folgt in Chiffretext C verschlüsselt:
Me mod n = 97 mod 143 = 48 = C
Wenn Alice die Nachricht von Bob erhält, entschlüsselt sie diese mit ihrem privaten RSA-Schlüssel (d, n) wie folgt:
Cd mod n = 48103 mod 143 = 9 = M
Um RSA-Schlüssel zum digitalen Signieren einer Nachricht zu verwenden, müsste Alice einen Hashwert - einen Message Digest ihrer Nachricht an Bob - erstellen, den Hashwert mit ihrem privaten RSA-Schlüssel verschlüsseln und den Schlüssel zur Nachricht hinzufügen. Bob kann dann überprüfen, ob die Nachricht von Alice gesendet und nicht verändert wurde, indem er den Hashwert mit ihrem öffentlichen Schlüssel entschlüsselt. Wenn dieser Wert mit dem Hashwert der ursprünglichen Nachricht übereinstimmt, kann nur Alice die Nachricht gesendet haben - Authentifizierung und Nichtabstreitbarkeit (Nonrepudiation) - und die Nachricht ist genau so, wie sie sie geschrieben hat – damit besteht Integrität.
Alice könnte ihre Nachricht auch mit Bobs öffentlichem RSA-Schlüssel verschlüsseln (Vertraulichkeit), bevor sie sie an Bob sendet. Ein digitales Zertifikat enthält Informationen, die den Eigentümer des Zertifikats identifizieren und auch den öffentlichen Schlüssel des Eigentümers enthalten. Zertifikate werden von der Zertifizierungsstelle, die sie ausstellt, signiert und können den Prozess der Beschaffung öffentlicher Schlüssel und der Überprüfung des Besitzers vereinfachen.

Wie sicher ist RSA?
Die Sicherheit von RSA beruht auf der Schwierigkeit, große ganze Zahlen zu faktorisieren. Mit zunehmender Rechenleistung und der Entdeckung effizienterer Faktorisierungsalgorithmen steigt auch die Fähigkeit, immer größere Zahlen zu faktorisieren.
Die Stärke der Verschlüsselung ist direkt mit der Schlüssellänge verbunden. Eine Verdoppelung der Schlüssellänge kann die Stärke exponentiell erhöhen, beeinträchtigt jedoch die Geschwindigkeit. RSA-Schlüssel sind in der Regel 1024 oder 2048 Bits lang, aber Experten sind der Meinung, dass 1024-Bit-Schlüssel nicht mehr gegen alle Angriffe völlig sicher sind.
Sofern kein unvorhergesehener Durchbruch im Quantencomputing erfolgt, wird es unter Umständen noch einige Zeit dauern, bis längere Schlüssel benötigt werden, aber die Elliptische-Kurven-Kryptografie (ECC) gewinnt bei vielen Sicherheitsexperten als Alternative zu RSA für die Kryptografie öffentlicher Schlüssel an Beliebtheit. Mit ihr können schnellere, kleinere und effizientere kryptografische Schlüssel erstellt werden.
Moderne Hardware und Software sind ECC-fähig, und die Popularität von ECC wird wahrscheinlich zunehmen. ECC kann eine gleichwertige Sicherheit bei geringerer Rechenleistung und geringerem Akkubedarf bieten und ist daher für mobile Anwendungen besser geeignet als RSA.







