Markov-Modell

Was ist ein Markov-Modell?

Ein Markov-Modell ist eine stochastische Methode für sich zufällig verändernde Systeme, die die Markov-Eigenschaft besitzen. Das bedeutet, dass der nächste Zustand zu einem bestimmten Zeitpunkt nur vom aktuellen Zustand abhängt und unabhängig von der Vergangenheit ist. Zwei gängige Arten von Markov-Modellen werden verwendet, wenn das darzustellende System autonom ist, das heißt, wenn das System nicht von einem externen Agenten beeinflusst wird. Diese sind:

1. Markov-Ketten. Dies ist die einfachste Art von Markov-Modellen und wird zur Darstellung von Systemen verwendet, bei denen alle Zustände beobachtbar sind. Markov-Ketten zeigen alle möglichen Zustände und zwischen den Zuständen die Übergangsrate, das heißt die Wahrscheinlichkeit, pro Zeiteinheit von einem Zustand in einen anderen zu wechseln. Zu den Anwendungen dieser Art von Modellen gehören die Vorhersage von Börsencrashs, Spracherkennung und Suchmaschinenalgorithmen.
2. Hidden-Markov-Modelle. Diese werden verwendet, um Systeme mit einigen unbeobachtbaren Zuständen darzustellen. Hidden-Markov-Modelle zeigen nicht nur Zustände und Übergangsraten, sondern auch Beobachtungen und Beobachtungswahrscheinlichkeiten für jeden Zustand. Hidden-Markov-Modelle werden für eine Reihe von Anwendungen verwendet, darunter Thermodynamik, Finanzen und Mustererkennung.

Zwei weitere häufig verwendete Arten von Markov-Modellen werden verwendet, wenn das dargestellte System kontrolliert wird, das heißt wenn das System von einem entscheidungsbefugten Agenten beeinflusst wird. Diese sind:

1. Markov-Entscheidungsprozesse. Diese werden verwendet, um die Entscheidungsfindung in diskreten, stochastischen, sequenziellen Umgebungen zu modellieren. Bei diesen Prozessen trifft ein Agent seine Entscheidungen auf der Grundlage zuverlässiger Informationen. Diese Modelle werden auf Probleme in den Bereichen künstliche Intelligenz (KI), Wirtschaft und Verhaltenswissenschaften angewandt.
2. Teilweise beobachtbare Markov-Entscheidungsprozesse. Sie werden in ähnlichen Fällen wie Markov-Entscheidungsprozesse verwendet, allerdings unter der Annahme, dass der Agent nicht immer über zuverlässige Informationen verfügt. Zu den Anwendungen dieser Modelle gehört die Robotik, wo es nicht immer möglich ist, den Standort zu kennen. Eine andere Anwendung ist die Maschinenwartung, bei der keine zuverlässigen Informationen über Maschinenteile eingeholt werden können, weil es zu kostspielig ist, die Maschine abzuschalten, um die Informationen zu erhalten.

Wie wird die Markov-Analyse angewendet?

Die Markov-Analyse ist eine probabilistische Technik, die Markov-Modelle verwendet, um das künftige Verhalten einer Variablen auf der Grundlage des aktuellen Zustands vorherzusagen. Die Markov-Analyse wird in vielen Bereichen eingesetzt, unter anderem in:

• Markov-Ketten werden für verschiedene Geschäftsanwendungen eingesetzt, zum Beispiel zur Vorhersage des Markenwechsels von Kunden im Marketing, zur Vorhersage der Verweildauer von Mitarbeitern im Personalwesen, zur Vorhersage der Zeit bis zum Ausfall einer Maschine in der Fertigung und zur Vorhersage des künftigen Aktienkurses im Finanzwesen.
• Die Markov-Analyse wird auch bei der Verarbeitung natürlicher Sprache (Natural Language Processing, NLP) und beim maschinellen Lernen (Machine Learning, ML) eingesetzt. Im NLP kann eine Markov-Kette verwendet werden, um eine Folge von Wörtern zu erzeugen, die einen vollständigen Satz bilden, oder ein verborgenes Markov-Modell kann für die Erkennung von Namen und die Kennzeichnung von Sprachbestandteilen verwendet werden. Beim maschinellen Lernen werden Markov-Entscheidungsprozesse verwendet, um die Belohnung beim bestärkenden Lernen (Reinforcement Learning) darzustellen.
• Ein Beispiel für den Einsatz der Markov-Analyse im Gesundheitswesen stammt aus Kuwait. Ein zeitkontinuierliches Markov-Kettenmodell wurde verwendet, um den optimalen Zeitpunkt und die optimale Dauer einer vollständigen COVID-19-Abriegelung im Land zu bestimmen, um sowohl neue Infektionen als auch Krankenhausaufenthalte zu minimieren. Das Modell ergab, dass eine 90-tägige Abriegelung, die 10 Tage vor dem Höhepunkt der Epidemie begann, optimal war.

Wie werden Markov-Modelle dargestellt?

Das einfachste Markov-Modell ist eine Markov-Kette, die in Gleichungen, als Übergangsmatrix oder als Diagramm dargestellt werden kann. Eine Übergangsmatrix wird verwendet, um die Wahrscheinlichkeit des Übergangs von jedem Zustand zu jedem anderen Zustand anzugeben. Im Allgemeinen werden die aktuellen Zustände in Zeilen aufgelistet und die nächsten Zustände in Spalten dargestellt. Jede Zelle enthält dann die Wahrscheinlichkeit des Übergangs vom aktuellen Zustand zum nächsten Zustand. Für eine beliebige Zeile müssen sich alle Zellwerte zu eins addieren.

Ein Graph besteht aus Kreisen, von denen jeder einen Zustand darstellt, und Richtungspfeilen, die mögliche Übergänge zwischen den Zuständen anzeigen. Die Richtungspfeile sind mit der Übergangswahrscheinlichkeit beschriftet. Die Übergangswahrscheinlichkeiten auf den Richtungspfeilen, die aus einem bestimmten Kreis kommen, müssen sich zu eins addieren.

Andere Markov-Modelle basieren auf der Kettendarstellung, enthalten aber zusätzliche Informationen, wie Beobachtungen und Beobachtungswahrscheinlichkeiten.

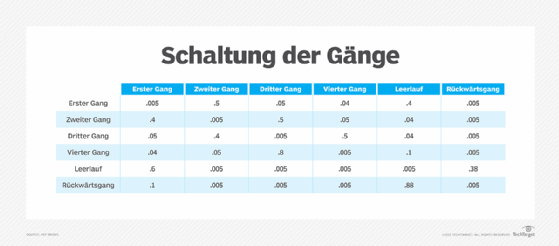
Die folgende Übergangsmatrix stellt das Schalten in einem Auto mit Schaltgetriebe dar. Es sind sechs Zustände möglich, und ein Übergang von einem bestimmten Zustand in einen anderen hängt nur vom aktuellen Zustand ab, das heißt, wohin das Auto vom zweiten Gang schaltet, hängt nicht davon ab, wo es vor dem zweiten Gang war. Eine solche Übergangsmatrix könnte aus empirischen Beobachtungen erstellt werden, die beispielsweise zeigen, dass die wahrscheinlichsten Übergänge vom ersten Gang in den zweiten oder den Leerlauf sind.

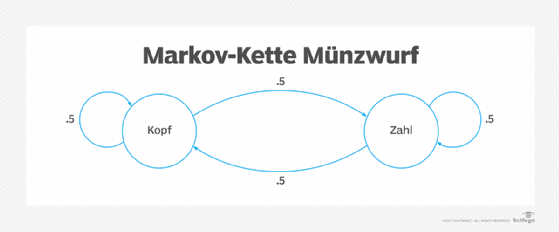
Die folgende Abbildung zeigt den Wurf einer Münze. Zwei Zustände sind möglich: Kopf und Zahl. Der Übergang von Kopf zu Kopf oder Kopf zu Zahl ist gleich wahrscheinlich (.5) und unabhängig von allen vorangegangenen Münzwürfen.

Geschichte der Markov-Kette

Markov-Ketten sind nach ihrem Schöpfer Andrej Andrejewitsch Markov benannt, einem russischen Mathematiker, der in den frühen 1900er Jahren einen neuen Zweig der Wahrscheinlichkeitstheorie rund um stochastische Prozesse begründete. Markov wurde stark von seinem Lehrer und Mentor Pafnuty Tschebyschow beeinflusst, der mit seinen Arbeiten ebenfalls neue Wege in der Wahrscheinlichkeitstheorie beschritt.