Integer

Ein Integer ist eine ganze Zahl (keine Bruchzahl), die positiv, negativ oder null sein kann

Beispiele für ganze Zahlen sind: -5, 1, 5, 8, 97 und 3.043.

Beispiele für nicht ganze Zahlen sind: -1,43, 1 3/4, 3,14, 0,09 und 5.643,1.

Die Gesamtmenge aller Integer-Zahlen Z wird formal folgendermaßen definiert:

Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}

In mathematischen Gleichungen werden unbekannte oder nicht spezifizierte Integer durch kleinere, kursiv geschriebene Buchstaben aus dem hinteren mittleren Teil des Alphabets dargestellt. Die häufigsten sind p, q, rund s.

Die Menge Z ist eine abzählbare Menge. Das heißt, die Zählbarkeit bezieht sich darauf, dass diese Elemente in einer Liste aufgeführt werden könnten, in der die Identität jedes Elements erhalten ist; und das, obwohl es eine unendliche Anzahl von Elementen in dieser Menge geben könnte.

Intuitiv ordnet man die Zahlen 356.804.251 und -67.332 den ganzen Zahlen zu, das heißt, man erkennt sie als Elemente der Liste {..., -3, -2, -1, 0, 1, 2, 3, ...}, wogegen die Zahlen 356.804.251,5, -67.332,89, -4/3 und 0,232323 als nicht dazu gehörend erkannt werden.

Die Elemente von Z können eins-zu-eins mit den Elementen von N, also der Menge der natürlichen Zahlen, gepaart werden, ohne dass Elemente aus einer der beiden Mengen herausgelassen werden.

Wenn N = {1, 2, 3, ...} ist, dann erfolgt die Paarung folgendermaßen:

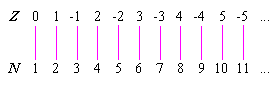
In unendlichen Zahlenräumen ist die Existenz einer eins-zu-eins-Korrelation der Lackmustest zur Bestimmung der Kardinalität (Mächtigkeit) oder Größe. Die Menge aller natürlichen Zahlen und die Menge aller rationalen Zahlen haben die gleiche Kardinalität wie Z. Allerdings haben reale Zahlen, imaginäre Zahlen und komplexe Zahlen eine größere Kardinalität als die von Z.

Nachfolgend eine Integer-Rap-Video (auf Englisch):