Fibonacci-Folge
Was ist die Fibonacci-Folge?
Die Fibonacci-Folge ist eine Reihe ganzer Zahlen (Fibonacci-Zahlen), die mit einer Null beginnt, gefolgt von einer Eins, dann von einer weiteren Eins und dann von einer Reihe stetig steigender Zahlen. Die Folge folgt der Regel, dass jede Zahl gleich der Summe der beiden vorangegangenen Zahlen ist.
Die Fibonacci-Folge beginnt mit den folgenden 14 ganzen Zahlen:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 ...
Jede Zahl, beginnend mit der dritten, entspricht der vorgeschriebenen Formel. Zum Beispiel gehen der siebten Zahl, 8, die Zahlen 3 und 5 voraus, die sich zu 8 addieren.
Die Folge kann theoretisch bis ins Unendliche fortgesetzt werden, wobei für jede neue Zahl dieselbe Formel verwendet wird. Einige Quellen zeigen, dass die Fibonacci-Folge mit einer Eins statt mit einer Null beginnt, aber das ist eher unüblich.
Berechnung der Fibonacci-Folge
Die Fibonacci-Folge kann mathematisch berechnet werden. Bei diesem Ansatz wird jede Zahl in der Folge als Term betrachtet, der durch den Ausdruck Fn dargestellt wird. Das n steht für die Position der Zahl in der Folge, beginnend mit Null. Zum Beispiel wird der sechste Term als F5 bezeichnet und der siebte Term als F6.
Mit dieser Nummerierung kann die Fibonacci-Folge durch die folgenden drei Gleichungen definiert werden:
- F0 = 0 (gilt nur für die erste ganze Zahl)
- F1 = 1 (gilt nur für die zweite ganze Zahl)
- Fn = Fn-1 + Fn-2 (gilt für alle anderen ganzen Zahlen)
Die ersten beiden Gleichungen besagen im Wesentlichen, dass der Term an der ersten Stelle gleich 0 und der Term an der zweiten Stelle gleich 1 ist. Die dritte Gleichung ist eine rekursive Formel, was bedeutet, dass jede Zahl der Folge durch die Verwendung der vorangegangenen Zahlen definiert wird. Um zum Beispiel die fünfte Zahl (F4) zu definieren, müssen die Terme F2 und F3 bereits definiert sein. Diese beiden Zahlen setzen wiederum voraus, dass die ihnen vorausgehenden Zahlen bereits definiert sind. Die Zahlen bauen in der Sequenz kontinuierlich aufeinander auf.
Die folgende Tabelle zeigt die Position jedes Terms zusammen mit seinem Fn-Wert und seiner Fibonacci-Zahl, beginnend mit dem ersten Term und endend mit dem vierzehnten Term.
| Position des Terms |
Fn-Wert |
Fibonacci-Zahl |
| 1. |
F0 |
0 |
| 2. |
F1 |
1 |
| 3. |
F2 |
1 |
| 4. |
F3 |
2 |
| 5. |
F4 |
3 |
| 6. |
F5 |
5 |
| 7. |
F6 |
8 |
| 8. |
F7 |
13 |
| 9. |
F8 |
21 |
| 10. |
F9 |
34 |
| 11. |
F10 |
55 |
| 12. |
F11 |
89 |
| 13. |
F12 |
144 |
| 14. |
F13 |
233 |
Sie können die Formel selbst ausprobieren, indem Sie die Tabelle verwenden, um die Zahlenfolge vor dem Wert des Zielterms zu ermitteln. Die folgende Berechnung ermittelt zum Beispiel die Fibonacci-Zahl für den Begriff an der zehnten Stelle (F9):
F9 = F9-1 + F9-2 = F8 + F7 = 21 + 13 = 34
Die Herausforderung bei einer rekursiven Formel besteht darin, dass sie immer die vorherigen Fibonacci-Zahlen voraussetzt, um eine bestimmte Zahl in der Folge zu berechnen. Zum Beispiel kann man den Wert des 100. Terms nicht berechnen, ohne den 98. und 99. Es gibt jedoch auch andere Gleichungen, die verwendet werden können, wie zum Beispiel die Binet-Formel, ein geschlossener Ausdruck zur Ermittlung der Zahlen der Fibonacci-Folge. Eine andere Möglichkeit besteht darin, die Logik der rekursiven Formel in einen Softwarecode zu programmieren, zum Beispiel in Java, Python oder PHP, und den Prozessor die Arbeit für Sie erledigen zu lassen.
Geschichte der Fibonacci-Folge
Die Fibonacci-Folge ist benannt nach Leonardo Pisano (auch Fibonacci genannt), einem italienischen Mathematiker, der von 1170 bis 1250 lebte. Fibonacci betrachtete die Sequenz als Antwort auf die folgende Frage:
Wie viele Kaninchenpaare werden in einem Jahr produziert, wenn man mit einem einzigen Paar beginnt und jedes Paar in jedem Monat ein neues Paar gebärt, das ab dem zweiten Monat produktiv wird?
Das Ergebnis kann numerisch ausgedrückt werden als 1, 1, 2, 3, 5, 8, 13, 21, 34 ...
Einem Sanskrit-Grammatiker, Pingala, wird die erste Erwähnung der Zahlenreihe zugeschrieben, die irgendwann zwischen dem fünften Jahrhundert v. Chr. und dem zweiten oder dritten Jahrhundert n. Chr. stattfand.
Seit Fibonacci die Zahlenreihe in die westliche Zivilisation eingeführt hat, hat sie von Zeit zu Zeit große Beachtung gefunden. In The Da Vinci Code ist die Fibonacci-Folge zum Beispiel Teil eines wichtigen Hinweises. Eine andere Anwendung, das Fibonacci-Gedicht, ist ein Gedicht, bei dem die Abfolge der Silbenzahlen pro Zeile dem Fibonacci-Muster folgt.
Fibonacci-Zahlen können auch zur Definition einer Spirale verwendet werden und sind für Biologen und Physiker von Interesse, da sie häufig bei verschiedenen natürlichen Objekten und Phänomenen zu beobachten sind. Die Verzweigungsmuster in Bäumen und Blättern und die Verteilung der Samen in einer Himbeere spiegeln beispielsweise die Fibonacci-Folge wider.
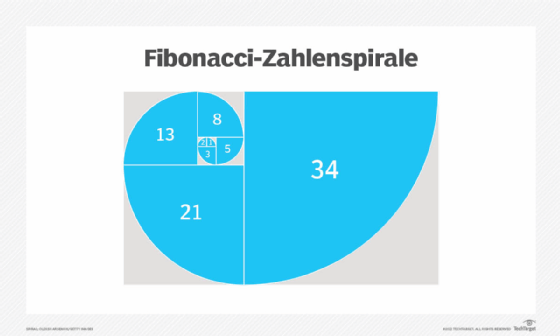
Die Fibonacci-Folge wird oft mit dem Goldenen Schnitt in Verbindung gebracht, einer Proportion (etwa 1:1,6), die in der Natur häufig vorkommt und in vielen Bereichen des menschlichen Handelns Anwendung findet. Sowohl die Fibonacci-Folge als auch der Goldene Schnitt werden unter anderem für die Gestaltung von Architektur, Websites und Benutzeroberflächen verwendet.










