Binär
Was ist binär?
Binär beschreibt ein Nummerierungsschema, bei dem es nur zwei mögliche Werte für jede Ziffer gibt – 0 oder 1 – und ist die Grundlage für alle in Computersystemen verwendeten Binärcodes. Diese Systeme verwenden diesen Code, um Betriebsanweisungen und Benutzereingaben zu verstehen und dem Benutzer eine entsprechende Ausgabe zu präsentieren.
Der Begriff binär bezieht sich auch auf jedes digitale Kodierungs-/Dekodierungssystem, in dem es genau zwei mögliche Zustände gibt. In der digitalen Datenspeicherung, -verarbeitung und -kommunikation werden die Werte 0 und 1 manchmal als niedrig beziehungsweise hoch bezeichnet. Bei Transistoren bedeutet 1 einen Stromfluss, während 0 keinen Stromfluss bedeutet.

Binär erklärt
Das binäre Zahlensystem wurde im 17. Jahrhundert von Gottfried Leibniz verfeinert. In der Mathematik und in Rechensystemen ist eine Binärziffer oder ein Bit die kleinste Einheit von Daten. Jedes Bit hat einen einzigen Wert, entweder 1 oder 0, was bedeutet, dass es keinen anderen Wert annehmen kann.
Computer können Zahlen mithilfe des Binärcodes in Form von digitalen 1en und 0en in der CPU und im Arbeitsspeicher (Memory, RAM) darstellen. Diese digitalen Zahlen sind elektrische Signale, die in der CPU oder im RAM entweder ein- oder ausgeschaltet sind.
Binär und Dezimal im Vergleich
Da das Binärsystem nur zwei Ziffern oder Bits verwendet und Zahlen mit unterschiedlichen Mustern von 1en und 0en darstellt, wird es als Basis-2-System bezeichnet. Dabei steht 1 für an (on) oder wahr, während 0 für aus (off) oder falschsteht.
Im Gegensatz dazu ist das Dezimalsystem ein Basis-10-System, bei dem jede mögliche Stelle in einer Zahl eine von 10 Ziffern sein kann (0-9). Bei einer mehrstelligen Zahl steht die Ziffer ganz rechts an erster Stelle, die Ziffer links daneben an zehnter Stelle, die Ziffer weiter links an hundertster Stelle und entsprechend weiterführend.
Beispiel
Bei der vierstelligen Zahl 1.980 stehen die einzelnen Ziffern an den folgenden Stellen.
| 1 | 9 | 8 | 0 |
| 1.000 Stelle | 1.00 Stelle | 10 Stelle | 1. Stelle |

Die Bedeutung des Binärcodes
Das binäre Zahlensystem ist die Grundlage aller Rechensysteme und -operationen. Es ermöglicht Geräten die Speicherung, den Zugriff und die Manipulation aller Arten von Informationen, die an die CPU oder das Memory gerichtet sind oder von dort kommen. Dies macht es möglich, Anwendungen zu entwickeln, die dem Benutzer folgende Möglichkeiten bieten:
- Websites anzeigen
- Dokumente erstellen und aktualisieren
- Spiele spielen
- Streaming-Videos und andere Arten von grafischen Informationen anzeigen
- auf Software zugreifen
- Berechnungen und Datenanalysen durchführen
Das binäre Schema von digitalen 1en und 0en bietet eine einfache und elegante Arbeitsweise für Computer. Es bietet auch eine effiziente Möglichkeit, logische Schaltungen zu steuern und die wahren (1) und falschen (0) Zustände eines elektrischen Signals zu erkennen.
Wie binäre Zahlen funktionieren
Das Binärsystem ist die Hauptsprache von Computersystemen. In diesen Systemen besteht eine Binärzahl aus einer Reihe von acht Bits. Diese Reihe wird als Byte bezeichnet. Im Binärschema bestimmt die Position der einzelnen Ziffern ihren Dezimalwert. Wenn man also die Position der einzelnen Bits kennt, kann man eine Binärzahl in eine Dezimalzahl umwandeln.
Bei Dezimalzahlen wird jede zusätzliche Stelle mit 10 multipliziert, wenn wir uns von rechts nach links bewegen (erste Stelle, 10. Stelle, 100. Stelle, und entsprechend höher). Bei Binärzahlen hingegen wird jede zusätzliche Stelle beim Übergang von rechts nach links mit zwei multipliziert. Die beiden folgenden Beispiele erläutern dieses Konzept.
Beispiel 1
So werden die Dezimalwerte für eine 8-Bit-Binärzahl (Byte) berechnet: 01101000.
Bei dieser Zahl steht die erste Ziffer ganz rechts und die achte Ziffer ganz links. Die zweite (0) bis siebte (1) Stelle werden von rechts nach links gelesen.
| Bit-Position |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| Bit |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
| Binär-zu-Dezimal-Berechnung (Exponent) |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
| Dezimaler Wert (x2) |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
Mit der Erhöhung der Bitposition von eins bis acht wird der vorherige Dezimalwert mit zwei multipliziert. Deshalb hat das erste Bit den Wert 1, das zweite Bit den Wert 2, das dritte Bit den Wert 4 und so weiter.
Der endgültige Wert der Dezimalzahl wird durch Addition der einzelnen Werte aus der obigen Tabelle berechnet. Es sollten jedoch nur die Werte addiert werden, bei denen das Bit gleich 1 ist. Diese Werte stellen die An-Stellung dar. Die 0 steht für die Aus-Stellung und wird daher bei der Berechnung des Dezimalwertes nicht mitgezählt.
Für die Binärzahl 01101000 wird der Dezimalwert also wie folgt berechnet:
8 + 32 + 64 = 104
Beispiel 2
So werden die Dezimalwerte für die Binärzahl 11111111 berechnet.
| Bit-Position |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| Bit |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| Binär-zu-Dezimal-Berechnung (Exponent) |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
| Dezimaler Wert |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
Bei dieser Binärzahl hat jedes Bit den Wert 1, so dass alle Einzelwerte addiert werden.
Der Dezimalwert für diese Zahl ist also wie folgt:
1 + 2 + 4 + 8 + 16+ 32 + 64 +128 = 255
Darstellung von Dezimalzahlen im Binärformat
Wie bereits erwähnt, funktioniert das binäre Zahlensystem nur mit 1en und 0en. Die Position dieser beiden Ziffern kann jedoch viel mehr Zahlen darstellen. Die Beispiele im vorigen Abschnitt zeigen, wie jede Dezimalzahl von 0 bis 255 mit Binärzahlen dargestellt werden kann. Zahlen, die größer als 255 sind, können auch durch Hinzufügen weiterer Bits zu einer 8-Bit-Binärzahl dargestellt werden.
Hier sind die Dezimalzahlen von Null bis 20 und ihre binären Entsprechungen.
| Dezimalzahl | Binärzahl | Dezimalzahl | Binärzahl |
| 0 | 0 | 11 | 1011 |
| 1 | 1 | 12 | 1100 |
| 2 | 10 | 13 | 1101 |
| 3 | 11 | 14 | 1110 |
| 4 | 100 | 15 | 1111 |
| 5 | 101 | 16 | 10000 |
| 6 | 110 | 17 | 10001 |
| 7 | 111 | 18 | 10010 |
| 8 | 1000 | 19 | 10011 |
| 9 | 1001 | 20 | 10100 |
| 10 | 1010 | --- |
--- |
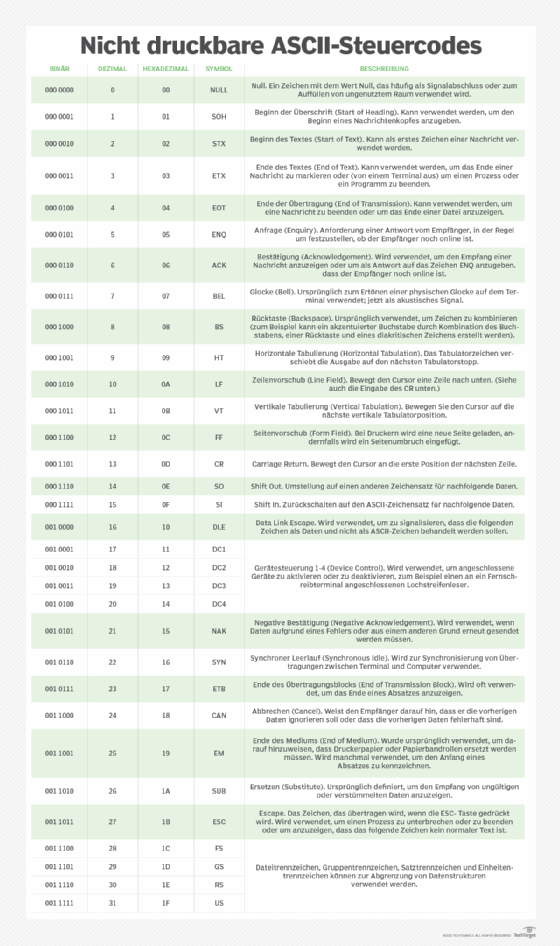
Umwandlung von Binärzahlen in Textzeichen
Binäre Zahlen können mit Hilfe des American Standard Code for Information Interchange (ASCII) in Textzeichen umgewandelt werden, um Informationen im RAM oder in der CPU des Computers zu speichern. ASCII-fähige Anwendungen, wie Textverarbeitungsprogramme, können Textinformationen aus dem RAM oder der CPU lesen. Sie können auch Textinformationen speichern, die dann vom Benutzer zu einem späteren Zeitpunkt abgerufen werden können. ASCII-Codes werden in der ASCII-Tabelle gespeichert, die aus 128 Text- oder Sonderzeichen besteht. Jedem Zeichen ist ein dezimaler Wert zugeordnet.
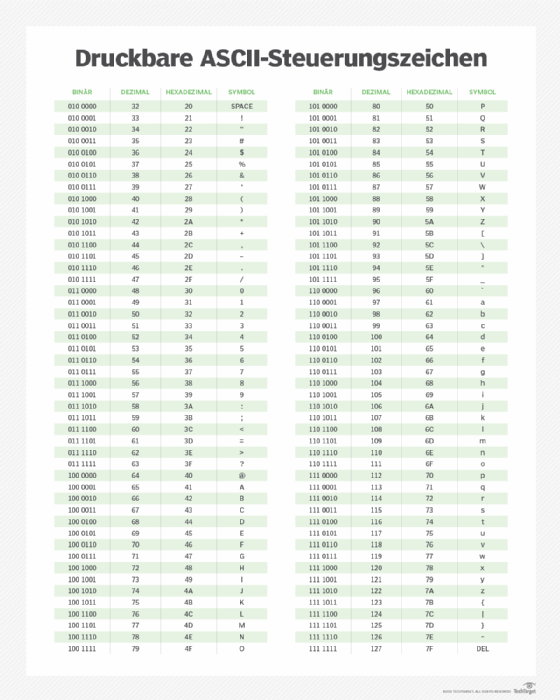
Im ersten Beispiel des vorherigen Abschnitts lautet die Binärzahl 01101000 (Dezimalzahl 104). In ASCII würde diese Zahl den Kleinbuchstaben h ergeben. Um Wörter zu bilden, müssen weitere Buchstaben zu h hinzugefügt werden. Binär ausgedrückt bedeutet dies, dass zur Binärzahl für h weitere Binärzahlen hinzugefügt werden.
Beispiel
Der Binärcode für ASCII-Kleinbuchstaben i ist 01101001. Um also das Wort hi zu bilden, wird die Binärzahl für i zur Binärzahl für h addiert. Dies ergibt die folgende Binärzahl
01101000 + 01101001 = 0110100001101001
In Dezimalzahlen ausgedrückt, sind die Dezimalzahlen für h und i 104 beziehungsweise 105.
Andere gängige Beispiele für Binärzahlen, die in ASCII-Textcode umgewandelt werden, sind die folgenden.
| Binärzahl | Dezimalzahl | ASCII Code |
| 110000 |
48 |
0 |
| 1000001 |
65 |
A (Großbuchstabe) |
| 1111111 |
127 |
DEL key |
| 11011 |
27 |
ESC key |









